Sketchnoting Resources, Challenges, and Tips

Sketchnoting: visual notes where ideas are conveyed through words, pictures, and visual elements

One of the things I love to do personally and with students is sketchnoting. I realized that while I've been great about sharing my sketchnoting journey, samples, and resources on Twitter, I really hadn't taken the time to make a post here, so it's time to fix that!

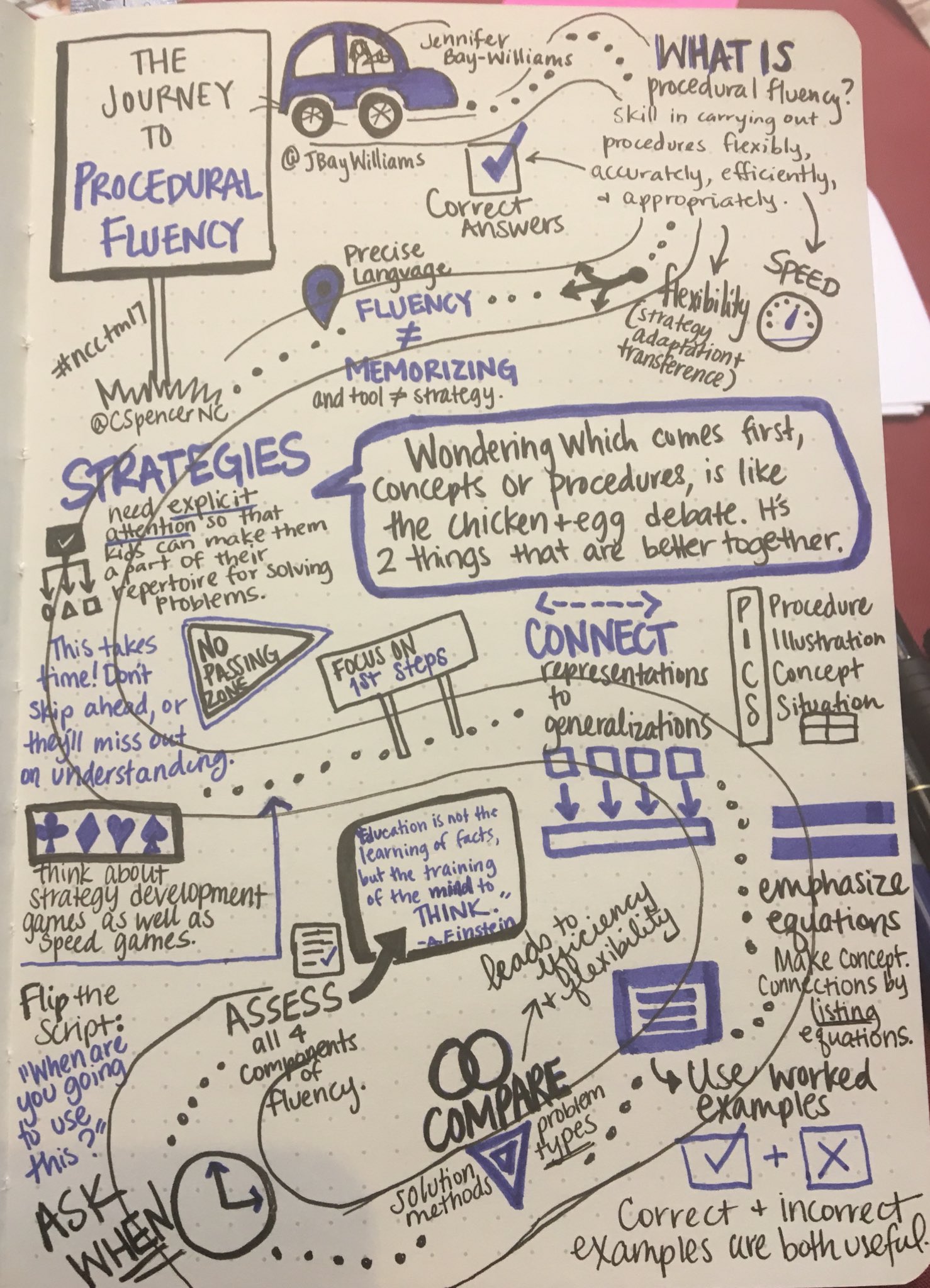
In July 2017, I had the chance to attend a workshop with Silvia Tolisano (@langwitches) on sketchnoting. While I'd heard the term, I only had a vague idea of what sketchnoting might look like. Silvia spoke of documenting learning, making thinking visible, and building connections through notetaking, and I was hooked. Here's my very first sketchnote from that workshop:

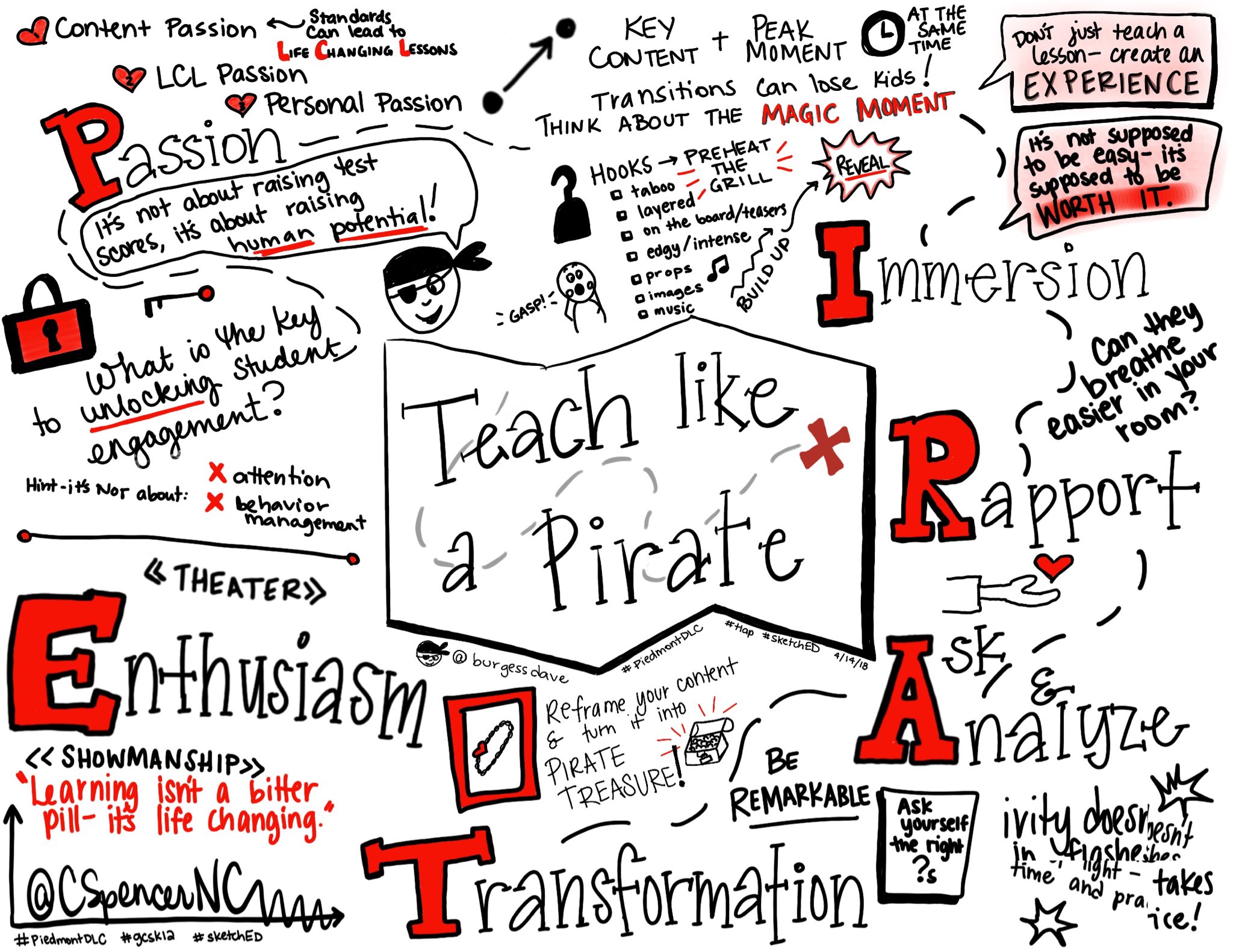
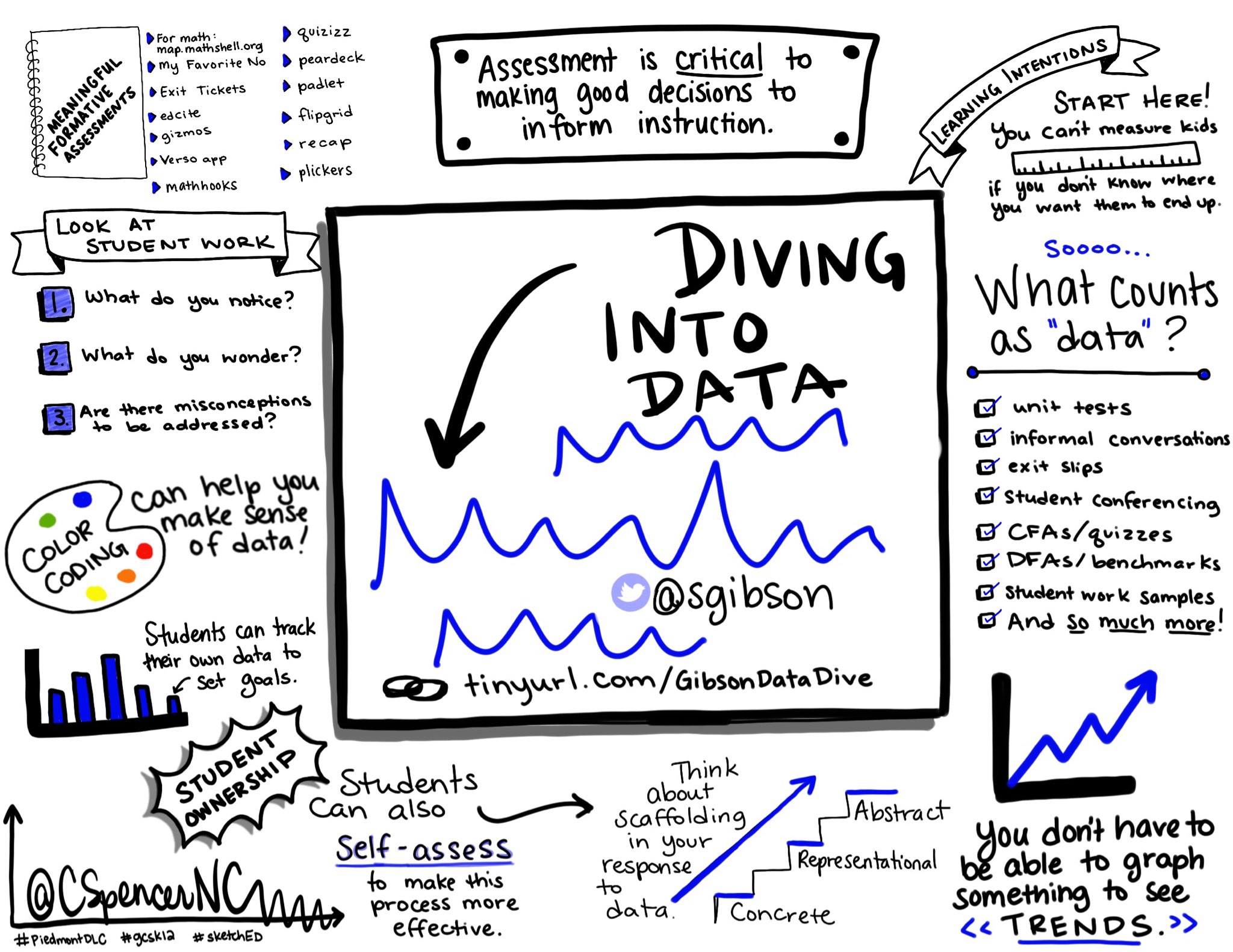
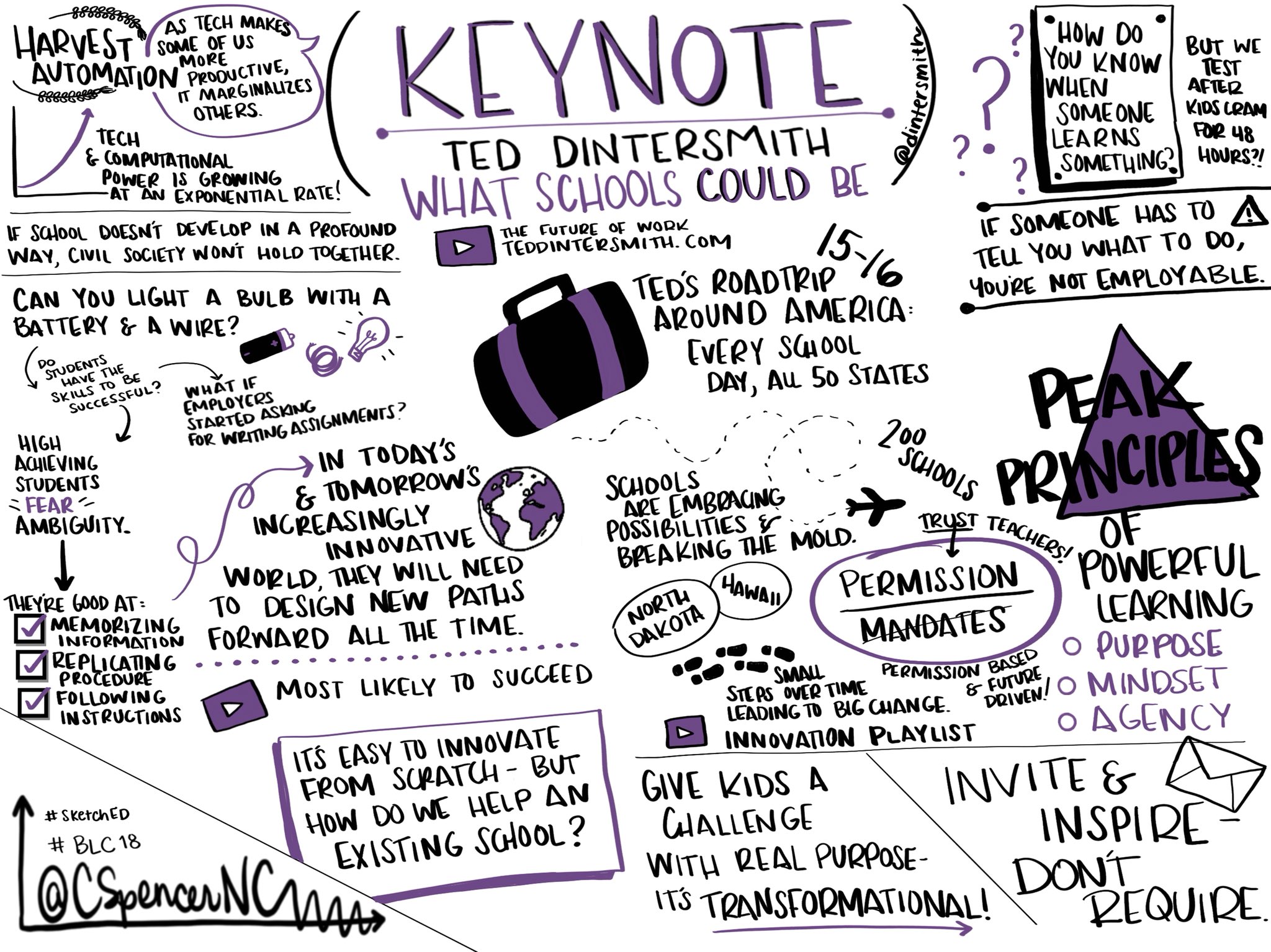
And let me tell you, I was STRESSED the whole way through making it. I wanted to use all of my pretty supplies, I wanted it to be perfect, and I was TERRIFIED of sharing it on Twitter. Since then, I've sketchnoted nearly every conference session, presentation, PD, and keynote I've attended. I've used sketchnoting with students across so many grade levels, and presented on sketchnoting over and over again. 

This technique that I once believed was so much about artwork and perfection...I've come to love it now that I know it's SOOOO not about those things. 

I love that sketchnoting is personalized, flexible, and fun! It lets you show connections and distinctions between different ideas, or rank things based on importance, or separate common content into small groups of information. 

Along the way, I stopped trying to use all of the markers at once:

 

Tried digital sketchnoting...(on an iPad Pro in ProCreate) 

 

...then promptly went back to paper 😂

And along with a few friends here in my district (especially the amazing @MrsYav), started up a sketchnoting Twitter account to help teachers use sketchnoting in their classrooms and encourage students along the way. It's @SketchnotEDU, and we also have a website where we store our PD materials (bit.ly/sketchnotEDU). 

The Twitter posts aren't as frequent as I'd like, but we do have some prompts and challenges dating back to early 2018. Some of my favorites were the skill challenges, and these remain my #1 tip for teachers trying to support student sketchnoting. 

Each week, pick a skill to work on and to incorporate into your notes. Consider its purpose - what it ADDS to the functionality or organization of the final set of notes, and use that function to guide your decisions of when to use it. 

These skills can be specific to sketchnoting, or can still be used with improving students' ability to take notes more traditionally. There's so much value in thinking about WHY bullet lists are useful, or why we might use arrows to connect topics or demonstrate order. Some of the skills challenges we posted on @SketchnotEDU included:

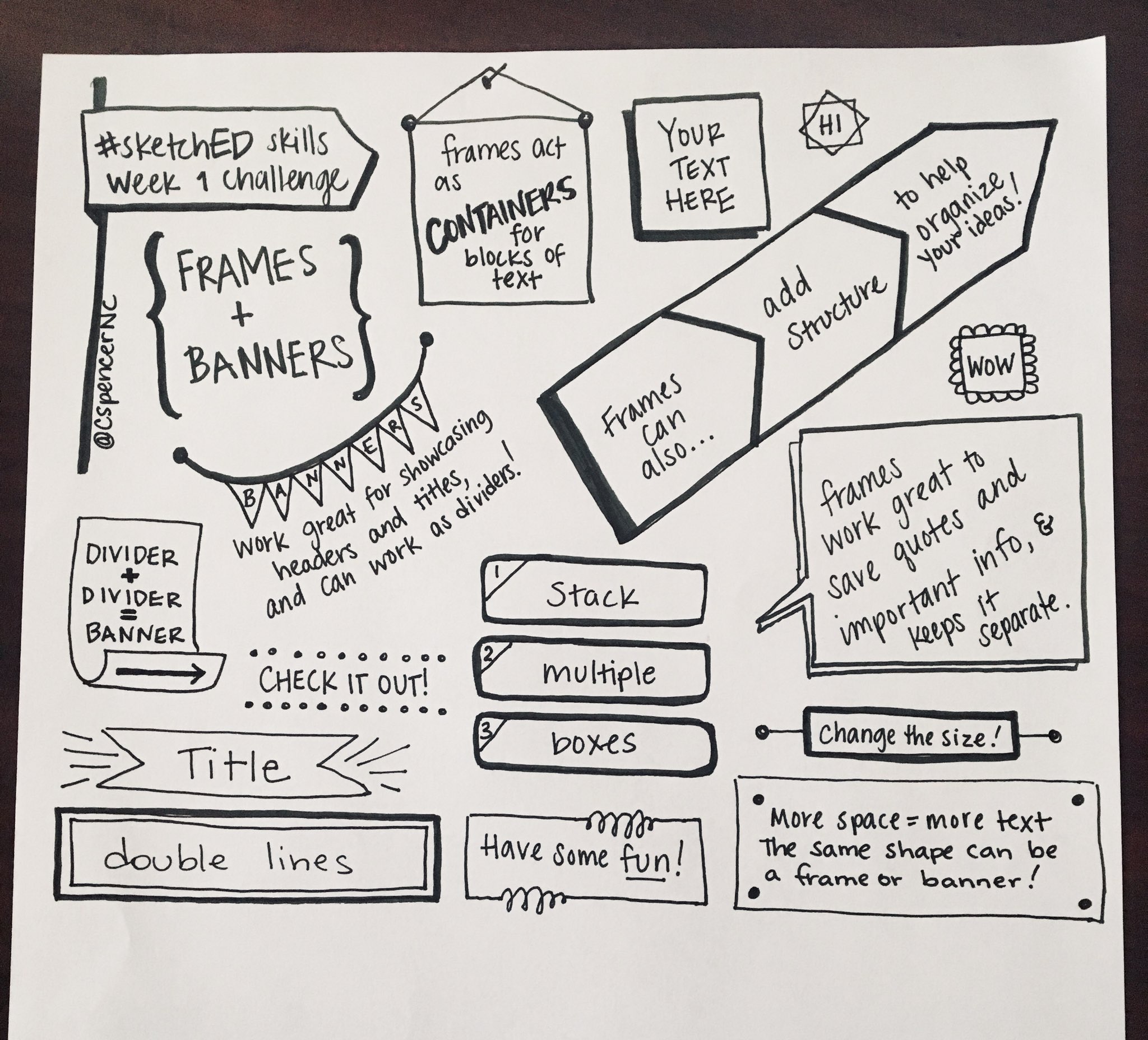
Banners and Frames

And the what-can-you-draw-with-just-lines-circles-triangles-dots-and-rectangles challenge!

There is so much research to support sketchnoting over outlining or traditional notes. I think my favorite thing though is that sketchnotes end up looking quite different for each student, which allows so many opportunities to share, compare, and discuss. 

One final tip, and I'll save the rest for future posts. This is actually for the same reason that I switched back to paper after trying digital sketchnoting, in addition to the fact that research supports paper notetaking over digital notetaking. 

USE PENS. OR MARKERS. DO NOT USE PENCIL. 

While sketchnoting, it's best if we all just forget that pencils exist for a little bit. The problem with pencils is that you've got the option to erase, fix, redo, and repeat. Mistakes are a part of math, a part of learning, and a part of sketchnotes. Sometimes you can turn them into a happy little bird, sometimes you just move on. But using pens or markers instead of pencils will make it so much easier to accept what ends up on the paper, and let go of trying to make everything perfect. 

Podcasts for PD

I've never really been a podcast gal. BUT lately, I've learned that it's about finding the right ones. And I've been thinking about how just listening to something can keep that topic on your mind all day, or sometimes all week.

There are a couple of AMAZING podcasts that I listen to regularly, and I wanted to share just how amazing they are.

1. Cult of Pedagogy: Just trust me. If you don't add a single other one, add this one. Jennifer Gonzalez is a former MS ELA teacher, and she has a way with words that will encourage you, challenge you, and inspire you in your journey as an educator. SOOO many amazing episodes. Her post was also how I heard about pineapple charts. We've implemented them digitally in our district in one of our PD groups, and it's so cool to be able to watch someone teach LIVE from across the county! (She also speaks to why we need to see each other teach, which I highly recommend.)
   
2. November Learning: Our district has been working for the last 2 years with Dr. Alan November and his team. His podcasts are few and far between, but the quality of information you'll get is incredible. I recommend starting with his talk with Dr. Rob Evans on Managing Change. #gamechanger
   
3. House of #EdTech: So many resources and great interviews! Start with Limited Tech? No Problem, or EdTech & Formative Assessment.
   
4. Truth for Teachers: Quick episodes, especially great for short errand runs or loading the dishwasher! ;) #107 on growth mindset is great, and I can't wait to listen to #115: "Goodbye Teacher Tired" that was just released.
   
   There are soooo many more. Other lists here and here.
   Also be sure to check out #PodcastPD on Twitter!
   
5. (for BONUS points) My fav podcasts for fun? Thanks for asking!
1. Harry Potter and the Sacred Text
2. Malcolm Gladwell's Revisionist History
3. Hidden Brain
4. Love to Sew
5. Levar Burton Reads

Number Sense Routines for High School

Hiya!

Welcome to the blog's new look! (I'm loving the clean, fresh feel...it's like spring cleaning, but for my screen, haha!)

I just wanted to take a quick moment today to share a Google site I built to house my favorite resources for number routines and building number sense for high school students.

We've all had students (or at least, I have!) that have been damaged in the past by teachers so concerned with a different recipe/procedure for every type of problem that their students end up uncomfortable thinking about numbers. There are plenty of quick, FUN activities that can build numeracy and just a bit of confidence, all while reinforcing classroom norms for discussion, collaboration, and problem-solving.

I even made this short link: tinyurl.com/HSnumeracy to make it easy to access. The site includes routines, links to number talks, & teacher info for implementing these types of activities and routines. There are even a few Global Math Department webinars to get you thinking! Did I mention that I love the new Google Sites? SO easy to use!

(And in case you're new around here, welcome! I've made a couple other collection websites in the past. One of my favorites is this Trello collection of review games & activities, from this post on Trello.)

Promoting Productive Struggle & Implementing Formative Assessment Lessons

We had an amazing meeting yesterday with our district's Math Design Collaborative yesterday for training on implementing FALs. One of the resources we went through was this article of 8 Teaching Habits that Block Productive Struggle in Math Students. It's kind of a what-not-to-do guide to teaching math. I also like that they paired it with this infographic poster of what to do instead. 

Our district is involved in a 3-year initiative with SREB, and I really couldn't possibly be more excited about this. Our best teachers have been selected (2 per school) to participate. We have teachers from every grade level 6-12, and from all types of schools. (Even our alternative school is participating!!)

During year 1, we have 8 days together as a group, and yesterday was Day 5. PD focuses on how to implement Formative Assessment Lessons (FALs), which are housed at map.mathshell.org. 

Now, when I was in the classroom, I was aware of this website, but hadn't implemented any of the lessons in their entirety. (To be REALLY REALLY honest, I had just stolen a few tasks and card sorts, and not used anything else.)

I had NO IDEA that all of the resources on this website are research based and are most effective (by far!) as complete lessons. 

Here's the basic idea, but you'll really get a better picture by reading through one of the scripted lessons. 

• FALs are separated into 2 categories:
• Concept Development (named based on content)
• Problem Solving (name based on context)
• Concept Development FALs are meant to be used one-half to two-thirds of the way through a unit. The goal is to figure out what kids know, what they don't know, and then use that to guide instruction (both through the remaining part of the unit, and to change how you teach that content next year). Sometimes these FALs also work at the beginning of a unit to review prerequisite content and guide the transition into new content. 
• Problem Solving FALs can be used any time during a unit, and are structured around really great problems with plenty of arguing potential. ;)

Here's the basic process to go through a FAL (I'll use a concept development FAL as an example, because so far it's the one I've worked with the most)

The day before the FAL: 

• Give the pre-assessment as an exit slip.
• That afternoon, sort the pre-assessments into 1,2, & 3 point piles (1 - little to no understanding, 2 - demonstrates some understanding, 3 - demonstrates understanding). Then use these piles to create homogeneous pairs of students (so the top 2 kids are paired together, then the next highest 2, etc). This isn't a formal grading process. 
• Once pairs are developed, and while the results on the pre-assessment are fresh in your mind, choose (or create) some feedback questions from the script. They should be based on the major misconceptions, obstacles, or gaps in learning you observed on the pre-assessments. 
• Make sure you have all materials & cards prepped and ready.

Day of the FAL:

• Follow the lesson script through the whole class intro, collaborative activity, sharing & whole class discussion, and then administer the post-assessment. 
• Whole class intro: usually involves white boards and some powerpoint slides. During this portion, you're just reminding kids of the work they did on the pre-assessment, and not "teaching." Just ask them some guiding questions to get them to notice differences in each other's responses. 
• Collaborative activity: when students work on activity (usually a card sort) in the pairs you designed based on their pre-assessment. Just give the time allotted in the script, and let go of the idea of completion. Just let each pair get as far as they can in the time given. During this time, project the feedback questions developed the day before.
• Sharing/Whole Class Discussion: usually involves some time to combine/change groups and compare answers, then a return to the whiteboards to discuss as a class. 
• Post-assessment is "graded" (but not really) the same way that the pre-assessment was, so that you can measure growth for each class.

My personal favorite FAL? Right now, it's Generating Polynomials from Patterns. 

Students use dot patterns to develop polynomial expressions for the white, black, and total dot patterns and WOW do they have to do some serious work with this one! It seriously challenges the advanced kiddos without being inaccessible for lower-achieving students.

Second runner up is Applying Properties of Exponents. I had a huge "AHA" moment with this one. How many times, when we're teaching laws of exponents, do we pretend like addition and subtraction of terms just cease to exist for a week or two? I'm definitely guilty. Here are the first few cards from this FAL so you can see what I'm talking about:

But if we choose not to shy away from types of problems that aren't immediately simplified using one application of one exponent property, our students are all the better for it. And this FAL does a phenomenal job of facing those obstacles, misconceptions, and gaps in learning square in the face.

Each of the FALs is designed to promote productive struggle in students. Each one is also designed to promote valuable, serious mathematical discourse. And that's something we should all strive to include more of in our classrooms.

And don't forget about the What-Not-To-Do and What-To-Do-Instead for Promoting Productive Struggle that I mentioned in the beginning of the post from the MIND Research Institute blog! 

Paper.li - Keeping up with the internet

There is just so much "out there" in the interwebs. 
Articles, tweets, ideas, pins, blog posts...

I use Bloglovin to keep up with the blog posts, but I only read through every couple of days. Which means some things fall through the cracks. Not to mention, it's only grabbing content from blogs I've already found. 

So I stumbled upon Paper.Li. 
I think someone must have tweeted it out with a #MTBoS hashtag, because I can't think of another way that I would have actually paid attention to it. But ever since, I keep finding new public paper.lis to follow! 

Basically, paper.li lets you build a newsletter out of tweets, articles, or basically anything out on the internet. It's really just a content collector. But I really like it because other people have built paper.lis that align with my interests. (I could build my own, but I feel like the ones I've found online are already so great that I don't need to.)

I keep the links on my bookmark bar, and when I get a free moment, I browse through a couple. I've found some new blogs to follow, and plenty of great ideas. Here's the list from my bookmarks bar:

The Math Education Daily

Math Daily

#Mathchat Daily

Teaching Science and Math Daily

Desmos Daily

Educational Technology Daily (Fridays only)

ELL Daily 

If you know of a great one I didn't list, please let me know! I really love finding new ideas, and this format just works for me. It kind of reminds me of Flipboard, but I never really found it useful because I didn't take the time to fill in all of my interests/fav blogs/etc. I like that with paper.li, I can just flip through everyone else's pages!

Content Literacy in Secondary Math

Wow - this blog's gotten a bit dusty. But here I am. Let's just pretend it's been 5 minutes instead of ... too long. 

I've been asked to work with a small group of teachers regarding content literacy strategies. We'll be meeting in groups of around 7 teachers (all math and science) during their planning periods. The school's improvement goal this year is to improve student performance on the ACT and English 2 state exam. The idea is to support that goal through implementation of some new strategies & some serious changes in expectations for reading and writing across the various content areas. 

I'll admit, I haven't done much work on this subject in math, but I'm excited to learn some new techniques and get to researching! Obviously, if we want students to have meaningful discourse and justify their thinking, we need to promote academic language and writing in our math classrooms.

Of course, my first thought was to check the TMC and GMD archives, but I didn't find very much. If you know of something I missed, please comment below!!

One of the articles I found listed 10 ways Literacy Can Promote a Deeper Understanding of Math.  I found it interesting that most of the items listed are things we do naturally in math class, but that it's important to formalize verbal explanations on paper. I thought a great "baby step" was to take discussions and put them online, which encourages students to write, edit, and read other responses. 

I also reached out to our county's SIOP & Differentiation coach. She does a training every semester on specific strategies for math to help our EL students. She has some incredible resources - check out her blog and resource site!

A couple of my favorite resources from her site are the Glossary of Strategies & Activities and the Bloom's Question Stems for ELs.  These resources are meant to support EL students, but the idea is that they're necessary for ELs, and beneficial for all students. I think so many times, it's easy to forget about this population within our schools. However, I'm trying to remember that ELs represent a microcosm of our larger student population when it comes to struggles with literacy and academic vocabulary. 

Link up any math content literacy resources/articles/etc you've got below! 

Using Mobiles to Solve Equations

This is a great idea for students to really show what they know with numbers and solving equations. 

I found the link on one of Resourceaholic's Gem lists. The post led me to Don Steward's Median blog. This is his activity. There are 3 posts: 'mobiles,' then 'mobile inequalities,' and finally 'mobile moments'.

I really like these activities! They are so adaptable to just about anything. Elementary students through high school students could work with adapted versions of these. Students do so much halving, doubling, sequencing, comparing, etc.

I can also see adapting this for fractions or decimals.

Maybe radians? Definitely integers...

This could even become an activity framework. It could be used for something like basic function notation, students evaluate to a number, then use that number to balance. (Almost as a self-check method)

Have a great weekend everyone!

UPDATE: There's also a website called SolveMe, which has these same types of problems, without numbers or expressions. It uses the same logic and reasoning skills, but with a bit friendlier interface. Here's the link.